Probability Distributions

Probability Distributions are used as an aid in Businesses while making Financial Risk Assessments, Inventory or Sales Forecasting, Annual Planning, etc. They are also used to determine the probability of demand for certain product or probability of number of people visiting the store in specific time interval and so on. This article mentions basic Discrete and Continuous Probability Distributions.

Discrete Probability Distributions

Discrete Probability Distributions are considered when experimental outcome or results of natural processes take finite number of values.

Bernoulli Distribution

It is associated with the experiments that have only two possible outcomes, a “success” and a “failure”. The probability of success is let’s say given by “p”. Since there are just two possible outcomes, the failure has probability of “1-p”. The probability distribution of Bernoulli trial for random variable X is given by

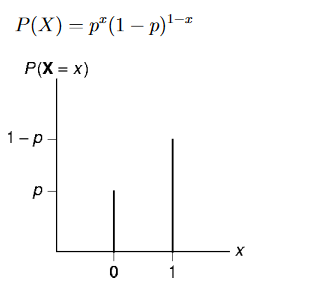
Binomial Distribution

The binomial distribution is related to the probability of “k” successes in a sequence of “n” independent Bernoulli trials. The Binomial Probability Distribution of “n” Bernoulli trials for random variable X resulting in “k” successes is given by

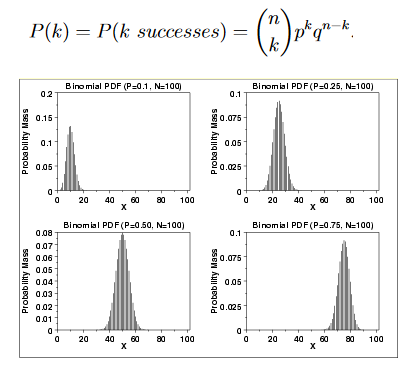
Geometric Distribution

The geometric distribution represents the probability of the first success occurring in the k^th trial. Thus first (k-1) independent trials resulted in a failure and the k^th trial is a success.  The Geometric Probability Distribution of “n” Bernoulli trials for random variable X resulting in success on k^th trial is given by

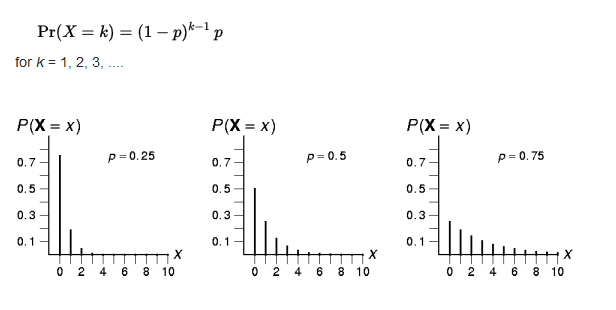
Negative Binomial Distribution

The Negative Binomial Distribution gives the probability of the kth success occurring in the xth trial of a Bernoulli process. Thus there must be (k-1) successes in the first (x-1) trials and the last trial must be a success. The probability distribution for this distribution is given by the following where p is probability of success and q is probability of failure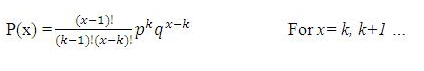

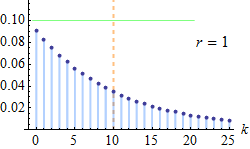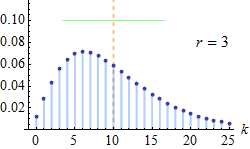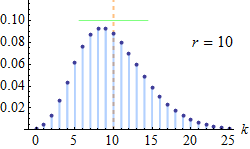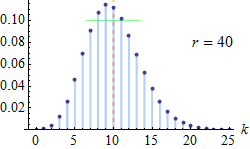
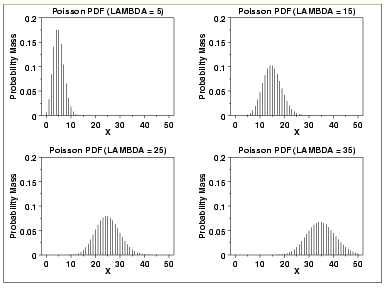
Poisson distribution

The Binomial distribution approaches the Poisson distribution as n becomes large such that “np” is a finite constant. For a distribution to assume Poisson distribution n is sufficiently large (n>50) and p is small (p<0.1).

Here “n” may be the number of time or space units into which a given time or space interval is divided. “r” is the number of successes in “n” trials.

Continuous Probability Distributions

In most of the cases the output from the natural processes or the experimental outcomes takes up infinite number of values.

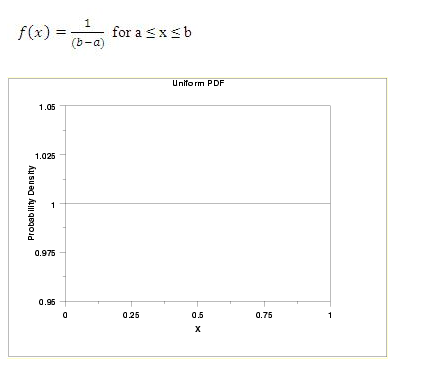
Uniform distribution

The uniform distribution is defined as

Negative Exponential Distribution

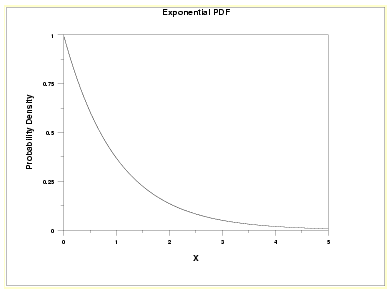
The negative exponential distribution is related to the discrete Poisson distribution. When an event occurrence follows the Poisson distribution the interval between the occurrences follows negative exponential distribution.

The probability density function for the Negative Exponential Distribution is defined as

Where λ is the rate of arrival from Poisson Distribution.

Normal Distribution

Normal distribution and its properties are useful in dealing with samples. It can be used for approximating other types of the probability distributions.

A continuous random variable X is said to have normal distribution if its pdf is as follows

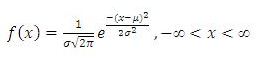
Properties of the Normal Distribution:

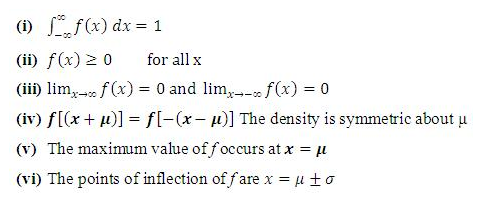
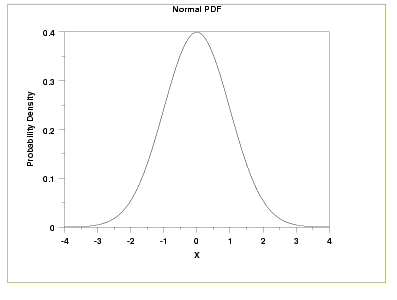
Log Normal Distribution

A random variable X is a Log Normal Random Variable if its probability density function is given by

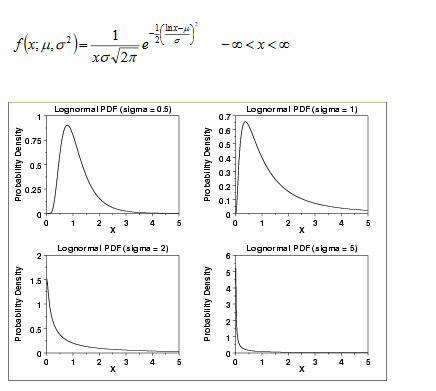
Beta Distribution

The Beta distribution is defined over the interval 0 to 1 and has 2 shape parameters a and b. If a RV takes on values between 0 & 1, its probability density function is described by the beta distribution given by

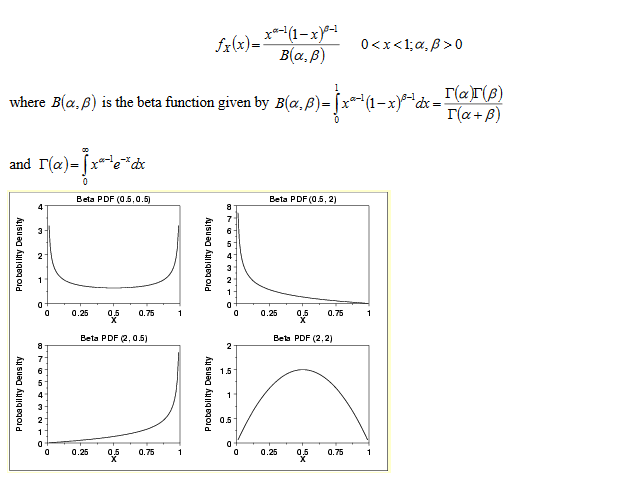
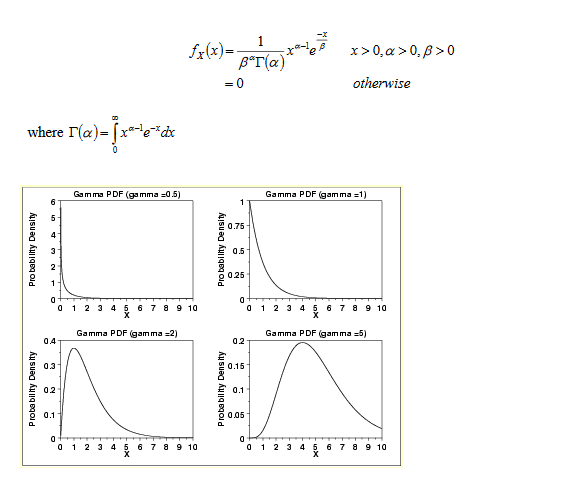
Gamma Distribution

Whenever the lower bound is zero, Gamma Distribution is used. The pdf of Gamma Distribution is given by

Sources and Reference:

http://www.nptel.ac.in/courses/105105138/6

http://www.itl.nist.gov/div898/handbook/eda/section3/eda366.htm

http://bluehawk.monmouth.edu/rclayton/web-pages/s05-525/sapd.html